MPI-AMRVAC 2.0 for Solar and Astrophysical Applications

The simplest hydrodynamical representation of the accretion of matter by a point mass was analyzed early on by Bondi (1952). It is an isotropic problem where only radial dependencies and components are considered. It describes how a non-zero temperature flow moving at a subsonic speed at infinity toward a central object of mass M_* can establish a steady, smooth, and transonic inflow solution. This unique continuous, transonic inflow solution v_r(r) does not display any shock. Provided the evolution is adiabatic, it means that the flow is isentropic: the pressure p(r) can be deduced from the mass density $\rho (r)$, using the fixed adiabatic index γ of the flow ($p{\rho }^{-\gamma }$ is independent of radius r). To illustrate how we make the equations dimensionless, let us look at the physical equation of conservation of the linear momentum:

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {v}_{r})}{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r}^{2})}{\partial r}+\displaystyle \frac{\partial p}{\partial r}=-\rho \displaystyle \frac{{{GM}}_{* }}{{r}^{2}},\end{eqnarray} \tag{ 1 }$$

where all quantities are in physical units, M_* is the mass of the accretor and G is the gravitational constant. We now adopt the following normalization quantities:

• 1.  
  the mass density at infinity, ${\rho }_{\infty }$,
• 2.  
  the sound speed at infinity, c_∞,
• 3.  
  the radius ${R}_{0}=2{{GM}}_{* }/{c}_{\infty }^{2}$.

Using these scalings, the mass per unit time crossing a sphere of a given radius (the mass accretion rate, $\dot{M}$), the pressure, and the time are normalized with ${\rho }_{\infty }{c}_{\infty }{R}_{0}^{2}$, ${\rho }_{\infty }{c}_{\infty }^{2}$, and ${R}_{0}/{c}_{\infty }$ respectively. In the equation above, if we replace ρ, v_r, p, r, and t with the product of a dimensionless number by the associated normalization quantity stated above (for instance ρ becomes $\tilde{\rho }\times {\rho }_{\infty }$), we obtain :

$$\begin{eqnarray}&&\displaystyle \frac{{\rho }_{\infty }{c}_{\infty }^{4}}{2{{GM}}_{* }}\left[\displaystyle \frac{\partial (\tilde{\rho }\tilde{{v}_{r}})}{\partial \tilde{t}}+\displaystyle \frac{1}{{\tilde{r}}^{2}}\displaystyle \frac{\partial ({\tilde{r}}^{2}\rho {\tilde{{v}_{r}}}^{2})}{\partial \tilde{r}}+\displaystyle \frac{\partial \tilde{p}}{\partial \tilde{r}}\right]\\ &&\quad =\,-\displaystyle \frac{{\rho }_{\infty }{c}_{\infty }^{4}}{4{({{GM}}_{* })}^{2}}\left[\displaystyle \frac{\tilde{\rho }{{GM}}_{* }}{{\tilde{r}}^{2}}\right],\end{eqnarray} \tag{ 2 }$$

which leads to the fully dimensionless equation (4) below. From now on, we omit the tildes and work exclusively with normalized dimensionless variables. Finally, notice that the analytic expressions below assume the specific case of a zero speed at infinity, but the conclusions below remain qualitatively the same in the general case.

The fundamental equations of this problem are the mass continuity equation

$$\begin{eqnarray}&&\displaystyle \frac{\partial \rho }{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r})}{\partial r}=0,\end{eqnarray} \tag{ 3 }$$

linear momentum conservation with gravity as a source term

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {v}_{r})}{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r}^{2})}{\partial r}+\displaystyle \frac{\partial p}{\partial r}=-\displaystyle \frac{\rho }{2{r}^{2}},\end{eqnarray} \tag{ 4 }$$

and the isentropic relation between (scaled) pressure and density as $p{\rho }^{-\gamma }={p}_{\infty }/({\rho }_{\infty }{c}_{\infty }^{2})=1/\gamma$. The steady-state solution admits a radius at which it becomes supersonic, called the sonic radius r_s, whose expression can be analytically derived to be ${r}_{s}=(5-3\gamma )/8$. The isothermal case (i.e., $\gamma =1$) has its associated sonic radius at ${r}_{s,0}=1/4$ (this is identical for the corresponding unique outflowing Parker isothermal wind solution). The normalized mass accretion rate can also be determined from the adiabatic index:

$$\begin{eqnarray}&&\dot{M}=\displaystyle \frac{\pi }{4}{\left(\displaystyle \frac{2}{5-3\gamma }\right)}^{\displaystyle \frac{5-3\gamma }{2(\gamma -1)}}.\end{eqnarray} \tag{ 5 }$$

For derivations of the above results, in the more general case of a non-zero subsonic speed at infinity, the reader might refer to Section 4.2 of El Mellah (2016). Below r = 1 (i.e., below the position of the scaling radius R₀) the properties of the flow significantly depart from their values at infinity. For an adiabatic index close to the maximum value of 5/3 that it can take, the sonic radius r_s becomes very small. We want to have the sonic radius within the simulation space, to have a trivial inner boundary treatment where inflow is supersonic. It then becomes advantagous to resort to a stretched mesh.

We work on domains extending from a radius of 0.01 (inner boundary) to 10 (outer boundary). We rely on a second-order two-step Harten–Lax–van Leer–Contact (HLLC) method (Toro et al. 1994), both for the predictor and the full time step, with the Koren slope limiter (Vreugdenhil & Koren 1993) used in the limited reconstruction of the primitive variables ρ and v_r, to obtain cell-face values. To design our initial conditions and fix the outer r = 10 inflow boundary conditions, we reformulate the fundamental equations to obtain a transcendental equation which indirectly gives the mass density as a function of radius r:

$$\begin{eqnarray}&&\displaystyle \frac{{\rho }^{\gamma -1}-1}{\gamma -1}-\displaystyle \frac{1}{2r}+\displaystyle \frac{{\dot{M}}^{2}}{32{\pi }^{2}}\displaystyle \frac{1}{{\rho }^{2}{r}^{4}}=0.\end{eqnarray} \tag{ 6 }$$

We numerically solve this relation with a Newton–Raphson method, which behaves correctly except very near the sonic radius where the algorithm may yield non-monotonous results. In this restricted region, we compute the mass density profile by linearly interpolating between points further away from the sonic radius. The obtained mass density profile is used as the initial condition and sets the fixed mass density in the ghost cells beyond r = 10. For the linear momentum $\rho {v}_{r}$, we deduce its radial profile from Equation (5) and similarly implement it both as initial condition and as forced outer boundary condition. For the inner boundary conditions, we copy the mass density in the ghost cells and then guarantee the continuity of the mass flux and Bernoulli invariant (as in El Mellah & Casse 2015). We then use MPI-AMRVAC to time-advance the solution to retrieve the stationary analytical solution, on three different kinds of radial spherical meshes :

• 1.  
  a non-stretched grid with a total number of cells N = 16388, without AMR,
• 2.  
  a stretched grid with a much reduced total number of cells (N = 132), stretched such that the relative resolution at the inner boundary remains the same as for the previous grid, without AMR,
• 3.  
  the same stretched grid as above, but with a total of five levels of mesh refinement, where blocks which contain the analytic sonic radius are refined. The refined grid is computed at the initial state and does not evolve thereafter (static AMR).

Within a few dynamical times, the profiles relax toward a numerical equilibrium close to the solution determined with the Newton–Raphson above. To quantify the relaxed steady states, we measure the position of the sonic radius obtained for each of the three meshes, and this for four different adiabatic indexes. The results are summarized in Figure 1. By eye, it is impossible to distinguish the numerically obtained sonic radii (dots) from the analytic solution (dashed curve) displayed in the upper panel, whatever the mesh. Therefore, we plotted the relative differences in the three lower panels for the non-stretched grid (b), a stretched grid (c), and a stretched grid with AMR (d). The error bars are evaluated by considering one hundredth of the spatial resolution in the vicinity of the sonic radius. We can conclude from those results that analytic sanity checks such as the position of the sonic radius are retrieved within a few tenths of percent with MPI-AMRVAC.

Zoom In Zoom Out Reset image size

Apart from this local agreement on the sonic point location, we can also quantify an error estimate for the entire relaxed mass density profiles obtained. For the case where $\gamma =1.4$, we compare runs with different AMR levels employing stretched meshes, to the relaxed mass density profile obtained with the non-stretched, high-resolution mesh above. We compute the L₂-norm between data points on stretched, AMR meshes and their counterpart on the non-stretched mesh (linearly interpolated to the same radial positions). Figure 2 shows that the matching between the solutions obtained increases as the number of maximum AMR levels rises.

Zoom In Zoom Out Reset image size

Radial stretching is introduced both to decrease the number of radial cells and, in two-dimensions (2D) and 3D, to prevent the deformation of cells when the radius of the inner radial boundary of the grid is orders of magnitude smaller than the radius of the outer boundary. To keep a constant cell aspect ratio all over a 2D $(r,\theta )$ grid, the radial step size ${\rm{\Delta }}{r}_{i}$ must obey the following relation :

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{\Delta }}{r}_{i}}{{r}_{i}{\rm{\Delta }}\theta }=\zeta \end{eqnarray} \tag{ 7 }$$

where r_i is the local radius, ${\rm{\Delta }}\theta$ the uniform angular step (the latitudinal one for a spherical $(r,\theta ,\varphi )$ mesh where θ is the colatitude) and ζ is a fixed aspect ratio. Since the radial step is then proportional to the radius, we obtain a kind of self-similar grid from the innermost to the outermost regions. We set the radial position r_i of the center of any cell indexed i mid-way between the two surrounding interfaces, ${r}_{i-1}$ and ${r}_{i+1}$, see Figure 3. The recursive relationship which builds up the sequence of radial positions for the cell centers is given by

$$\begin{eqnarray}&&{r}_{i+1}={r}_{i}+\displaystyle \frac{{\rm{\Delta }}{r}_{i}}{2}+\displaystyle \frac{{\rm{\Delta }}{r}_{i+1}}{2},\end{eqnarray} \tag{ 8 }$$

where ${\rm{\Delta }}{r}_{i}$ is the radial step of cell i. Inserting equation (7) yields :

$$\begin{eqnarray}&&{r}_{i+1}={{qr}}_{i}\quad \mathrm{where}\quad q=\displaystyle \frac{1+\zeta {\rm{\Delta }}\theta /2}{1-\zeta {\rm{\Delta }}\theta /2}.\end{eqnarray} \tag{ 9 }$$

Hereafter, q is called the scaling factor. We fix the radii of the inner and outer radial boundaries of the domain, r_in and r_out respectively, along with the total number of cells in the radial direction N (excluding the ghost cells). The scaling factor is then computed from equation (9) applied to the two boundaries: $q={({r}_{\mathrm{out}}/{r}_{\mathrm{in}})}^{1/N}$. We can derive the required aspect ratio for a radially stretched grid:

$$\begin{eqnarray}&&\zeta =\displaystyle \frac{2(q-1)}{{\rm{\Delta }}\theta (q+1)}.\end{eqnarray} \tag{ 10 }$$

For a stretching smooth enough and a usual number (typically two) of ghost cells, the radial positions of the inner ghost cells remain positive.

Zoom In Zoom Out Reset image size

As should be clear from our example applications, the stretched grid is created accordingly to the type of symmetry (cylindrical or spherical) and to the dimensionality (1D, 2D, or 3D). The numerical schemes incorporate the variable radial step size where needed. The coupling between stretched grids and block-based AMR has been made possible by computing a scaling factor for each AMR level. Since children blocks at the next level span the same radial range as the mother block but with twice as many cells, the scaling factor ${q}_{l+1}$ of the children blocks at level $l+1$ can be obtained from the scaling factor q_l of the mother block at level l via ${q}_{l+1}=\sqrt{{q}_{l}}$.

The time gain can be estimated by writing the ratio of the number of radial cells in a non-stretched versus a stretched grid, with the same absolute radial step at the inner boundary. It approximately amounts to:

$$\begin{eqnarray}&&{\rm{\Lambda }}\sim \displaystyle \frac{{r}_{\mathrm{out}}/{r}_{\mathrm{in}}}{2{\mathrm{log}}_{10}({r}_{\mathrm{out}}/{r}_{\mathrm{in}})}\end{eqnarray} \tag{ 11 }$$

which quickly rises when ${r}_{\mathrm{out}}/{r}_{\mathrm{in}}$ exceeds a few tens. Moreover, in combination with AMR, the stretched grid enables us to resolve off-centered features (see, e.g., our 3D application in Section 2.4), without lowering the time step, if the latter is dominated by dynamics within the innermost regions. In the previous section on 1D Bondi accretion, the number of cells for an accurate solution could be reduced by two orders of magnitude.

A truly 2D accretion-type problem is the Bondi–Hoyle–Lyttleton (BHL) model designed by Hoyle & Lyttleton (1939) and Bondi & Hoyle (1944) (for a more detailed review of the BHL model and its refinements, see Edgar 2004; El Mellah 2016). The major change with respect to the 1D Bondi flow is that there is now a supersonic bulk planar motion of the flow with respect to the accretor, at speed ${v}_{\infty }\gt {c}_{\infty }$, which has two serious consequences:

• 1.  
  the geometry of the problem is no longer isotropic but is still axisymmetric (around the axis through the accretor and with direction set by the speed of the inflow at infinity),
• 2.  
  since the flow is supersonic at infinity, there can be a bow shock induced by the interaction with the accretor. The isentropic assumption we used to bypass the energy equation in Section 2.1 no longer holds.

Analytic considerations point to a formation of the shock at a spatial scale of the order of the accretion radius ${R}_{\mathrm{acc}}=2{{GM}}_{* }/{v}_{\infty }^{2}$. This radius is close to the size of the accretor, when we study stars accreting the wind of their companion in binary systems (Chen et al. 2017). However, for compact accretors which have an associated Schwarzschild radius ${R}_{\mathrm{sch}}=2{{GM}}_{* }/{c}^{2}$, the contrast between accretor size and the scale at which the flow is deflected by the gravitational influence of the accretor becomes important, since

$$\begin{eqnarray}&&\displaystyle \frac{{R}_{\mathrm{acc}}}{{R}_{\mathrm{sch}}}={\left(\displaystyle \frac{c}{{v}_{\infty }}\right)}^{2},\end{eqnarray} \tag{ 12 }$$

where c is the speed of light. For realistic speeds ${v}_{\infty }$ of stellar winds in wind-dominated X-ray binaries for instance, it means that the accretor is 4 to 5 orders of magnitude smaller than the shock forming around it. To bridge the gap between those scales, a stretched grid is mandatory.

This has been done with MPI-AMRVAC in El Mellah & Casse (2015), where we solved the hydro equations on a 2D $(r,\theta )$ grid combined with axisymmetry about the ignored φ direction. The set of equations to solve now include the energy equation, also with work done by gravity appearing as a source term, where the energy variable $E=p/(\gamma -1)+\rho ({v}_{r}^{2}+{v}_{\theta }^{2})/2$ is used to deduce the pressure. In the simulations, we work with an adiabatic index representative of a monoatomic gas, $\gamma =5/3$. The equations solved write as:

$$\begin{eqnarray}&&\displaystyle \frac{\partial \rho }{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r})}{\partial r}+\displaystyle \frac{1}{r\sin \theta }\displaystyle \frac{\partial (\rho {v}_{\theta }\sin \theta )}{\partial \theta }=0,\end{eqnarray} \tag{ 13 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {v}_{r})}{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r}^{2})}{\partial r}+\displaystyle \frac{1}{r\sin \theta }\displaystyle \frac{\partial (\rho {v}_{r}{v}_{\theta }\sin \theta )}{\partial \theta }\\ &&\quad +\displaystyle \frac{\partial p}{\partial r}=\displaystyle \frac{\rho {v}_{\theta }^{2}}{r}-\displaystyle \frac{\rho }{2{r}^{2}},\end{eqnarray} \tag{ 14 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {v}_{\theta })}{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}\rho {v}_{r}{v}_{\theta })}{\partial r}+\displaystyle \frac{1}{r\sin \theta }\displaystyle \frac{\partial (\rho {v}_{\theta }^{2}\sin \theta )}{\partial \theta }\\ &&\quad +\displaystyle \frac{1}{r}\displaystyle \frac{\partial p}{\partial \theta }=-\displaystyle \frac{\rho {v}_{r}{v}_{\theta }}{r},\end{eqnarray} \tag{ 15 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial E}{\partial t}+\displaystyle \frac{1}{{r}^{2}}\displaystyle \frac{\partial ({r}^{2}(E+p){v}_{r})}{\partial r}+\displaystyle \frac{1}{r\sin \theta }\\ &&\quad \times \displaystyle \frac{\partial [(E+p){v}_{\theta }\sin \theta ]}{\partial \theta }=-\displaystyle \frac{\rho {v}_{r}}{2{r}^{2}}.\end{eqnarray} \tag{ 16 }$$

The terms on the RHS are handled in geometric and gravitational source terms.

Fortunately, not all quantities require an inner r_in boundary which matches the physical size of the accretor. For instance, Ruffert (1994) quantified the impact of the size of the inner boundary r_in on the measured mass accretion rates at the inner boundary, ${\dot{M}}_{\mathrm{in}}$ (see Figure 5.3 in El Mellah 2016). The result is that ${\dot{M}}_{\mathrm{in}}$ matches the analytic value provided one reaches the sonic radius. But, as explained in the previous 1D Bondi test, and as can be seen in Figure 1, the sonic radius drops to zero for $\gamma =5/3$. Ruffert (1994) showed that to retrieve the analytic value of the mass accretion rate within a few percent, r_in must be below a hundredth of the accretion radius. Therefore, in the simulations where $\gamma =5/3$, we need to span at least 3 orders of magnitude: while the outer boundary lies at 8R_acc, the inner boundary has a radius of a thousand times the accretion radius. With a resolution of 176 × 64 cells in the $(r,\theta )$ plane (without the ghost cells), it gives an aspect ratio of 1.04 (and a scaling factor of 1.05).

The steady solution has the supersonic planar outflow upstream, suddenly transitioning to a subsonic inflow at the bow shock. Then, part of this now subsonic inflow is still accreted in a continuous Bondi-type transonic fashion in the wake of the accretor. Solutions for different Mach numbers ${{ \mathcal M }}_{\infty }={v}_{\infty }/{c}_{\infty }$ of the supersonic planar inflow are compared in Figure 4, showing density variations in a zoomed-in fashion. The upstream conditions at 8R_acc are set by the ballistic solutions (Bisnovatyi-Kogan et al. 1979) and the downstream boundary condition is continuous (with a supersonic outflow). At the inner boundary, we enforce the same boundary conditions as described in Section 2.1, with a continuous ${v}_{\theta }$. MPI-AMRVAC provides a steady solution on a stretched (non-AMR) grid which matches the orders of magnitude mentioned above: the position of the detached bow shock, the jump conditions at the shock, as well as the inner mass accretion rate (El Mellah & Casse 2015). In particular, we retrieve a topological property derived by Foglizzo & Ruffert (1996) concerning the sonic surface, deeply embedded in the flow and anchored into the inner boundary, whatever its size (see the solid black contour denoting its location in the zoomed views in Figure 4).

Zoom In Zoom Out Reset image size

A third hydrodynamic application of radially stretched AMR grids generalizes the 2D (spherical axisymmetric) setup above to a full 3D case. In a forthcoming paper (I. El Mellah et al. 2018, in preparation), we use a full 3D spherical mesh to study wind-accretion in supergiant X-ray binaries, where a compact object orbits an evolved mass-losing star. In these systems, the same challenge of scales identified by Equation (12) is at play, and the BHL shock-dominated, transonic flow configuration is applicable. In realistic conditions, the wind of the evolved donor star is radiatively driven and clumpy, making the problem fully time-dependent. We model the accretion process of these clumps onto the compact object, where the inhomogeneities (clumps) in the stellar wind enter a spherically stretched mesh centered on the accreting compact object, and the clump impact on the time-variability of the mass accretion rate is studied. The physics details will be provided in that paper; here we emphasize how the 3D stretched AMR mesh is tailored to the problem at hand. The initial and boundary conditions are actually derived from the 2.5D solutions described above, while a seperate 2D simulation of the clump formation and propagation in the companion stellar wind serves to inject time-dependent clump features in the supersonic inflow.

The use of a 3D spherical mesh combined with explicit time stepping brings in additional challenges since the time step ${\rm{\Delta }}t$ must respect the Courant–Friedrich–Lewy (CFL) condition. Since the azimuthal line element is $r\sin \theta {\rm{\Delta }}\varphi$ with colatitude θ, it means that the time step obeys

$$\begin{eqnarray}&&{\rm{\Delta }}t(\theta )\propto \sin (\theta ).\end{eqnarray} \tag{ 17 }$$

The axisymmetry adopted in the previous section avoided this complication. As a consequence, the additional cost in terms of number of iterations to run a 3D version of the setup presented in the previous section is approximately

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{\Delta }}t(\pi /2)}{{\rm{\Delta }}t({\theta }_{\min })}\sim \displaystyle \frac{1}{{\theta }_{\min }},\end{eqnarray} \tag{ 18 }$$

where ${\theta }_{\min }\ll \pi /2$ is the colatitude of the first cell center just off the polar axis. For a resolution on the base AMR level of 64 cells spanning $\theta =0$ to $2\pi$, it means a time step 40 times smaller compared to the 2D counterpart. Together with the additional cells in the azimuthal direction, this makes a 3D setup much more computationally demanding.

We compromise on this aspect by using an AMR mesh which deliberately exploits a lower resolution at the poles, while still resolving all relevant wind structures. Since the clumps embedded in the supersonic inflow are small-scale structures, we need to enable AMR (up to four levels in the example of Figure 5) in the upstream hemisphere to resolve them, in particular at the outer edge of the mesh where the radially stretched cells have the largest absolute size on the first AMR level. At the same time, we are only interested in the fraction of the flow susceptible to be accreted by the compact object, so we can inhibit AMR refinement in the downstream hemisphere, except in the immediate vicinity of the accretor (below the stagnation point in the wake). We also prevent excessive refinement in the vicinity of the accretor (no refinement beyond the third level in Figure 5) since the stretching already provides more refined cells. Finally, in the upstream hemisphere, we favor AMR refinement in the accretion cylinder, around the axis determined by the direction of the inflow velocity. Note that this axis was the symmetry polar axis in the previous 2.5D setup in Section 2.3, but this is different in the present 3D setup, where the polar axis is above and below the central accretor. In the application to study supergiant X-ray binary accretion, together with geometrically enforced AMR, we use dynamic AMR with a refinement criterion on the mass density to follow the flow as it is accreted onto the compact object.

Zoom In Zoom Out Reset image size

To simulate the propagation of the solar wind between the Sun and the orbit of the Earth (at 215 ${R}_{\odot }$), the use of a spherical stretched grid can also be very important. First, it considerably reduces the amount of cells needed in the simulations (by a factor of 46). Second, it allows us to maintain the same aspect ratio for all the cells in the simulation. We present here the results of 2.5D MHD simulations of the meridional plane of the solar wind, i.e., axisymmetric simulations on a 2D mesh where the three vector components are considered for the plasma velocity and for the magnetic field. This simulation setup also allows us to test the magnetic field splitting (MFS) method discussed in Section 3. Instead of solving the induction equation for the total magnetic field (${\boldsymbol{B}}$), one can solve it for the difference with the internal dipole field of the Sun (${{\boldsymbol{B}}}_{1}={\boldsymbol{B}}-{{\boldsymbol{B}}}_{0}$), where ${{\boldsymbol{B}}}_{0}$ represents the dipole field. We will here compare the results of these two setups. In our simulations, the solar wind is generated through the inner boundary (at r = 1 ${R}_{\odot }$), in a fashion similar to Jacobs et al. (2005) and Chané et al. (2005, 2008): the temperature is fixed to $1.5\times {10}^{6}$ K, and the number density to $1.5\times {10}^{6}$ cm⁻³, where the azimuthal velocity is set to $(2.09-0.264{\cos }^{2}\theta -0.334{\cos }^{4}\theta )\sin \theta$ km s⁻¹ to enforce the solar differential rotation of the Sun (θ is the colatitude), and where the radial component of the magnetic field is fixed to the internal dipole value (with B_r = 1.1 G at the equator). In addition, close to the equator (at latitudes lower than $22\buildrel{\circ}\over{.} 6$), in the streamer region, a dead zone is enforced at the boundary by fixing the radial and the latitudinal velocities to zero. The equations solved are the ideal MHD equations plus two source terms: one for the heating of the corona and one for the gravity of the Sun. The heating of the corona is treated as an empirical source term in the energy equation. We follow the procedure described in Groth et al. (2000) with a heating term dependent on the latitude (with a stronger heating at high latitudes) and on the radial distance (the heating decreases exponentially). The inclusion of this source term results in a slow solar wind close to the equatorial plane and a fast solar wind at higher latitudes (see Figure 6).

Zoom In Zoom Out Reset image size

The simulations are performed on a spherical stretch mesh between 1 ${R}_{\odot }$ and 216 ${R}_{\odot }$ with 380 cells in the radial direction and 224 cells in the latitudinal direction. For these simulations, we do not take advantage of the AMR capabilities of the code and a single mesh level is used (no refinement). The smallest cells (close to the Sun) are 0.014 ${R}_{\odot }$, while the largest cells (at 1 au) are 3 ${R}_{\odot }$. The equations are solved with a finite-volume scheme, using the two-step HLL solver (Harten et al. 1983) with Koren slope limiters. Powell's method (Powell et al. 1999) is used for the divergence cleaning of the magnetic field. The adiabatic index γ is set to 5/3 in these simulations.

The results of the simulations are shown in Figure 6. The top panels display the plasma density, the velocity vectors, the magnetic field lines, and the Alfvén surface. One can see that both panels are very similar with: (1) a fast solar wind at high latitudes and a slow denser wind close to the equatorial plane, (2) a dense helmet streamer (the reddish region close to the equatorial plane) close to the Sun where the plasma velocity is almost zero, and (3) an Alfvén surface located between 4 and 7.5 ${R}_{\odot }$ in both cases. To highlight the differences between the two simulations, 1D cuts at 1 au are provided in the lower panels of Figure 6 for both simulations. The density profiles are very similar, but the density is marginaly lower when the MFS method is used. For both simulations, the solar wind is, as expected, denser close to the equatorial plane and displays densities in agreement with the average measured density at 1 au. The radial velocity profiles (shown in the middle panel) are nearly identical almost everywhere in both simulations, with a fast solar wind (a bit less than 800 km s⁻¹) at high latitudes, and a slow solar wind (a bit less than 400 km s⁻¹) close to the equator. The only region where the radial velocity profiles marginally differ is on the equatorial plane, where the radial velocity is 4% higher when the MFS method is used. These results are very similar to in situ measurements at 1 au (see, for instance, Phillips et al. 1995). Although the differences are more pronounced for the magnetic field magnitude (right panel), they never exceed 10%. In general, the differences between the two simulations are negligible.

Here, we demonstrate this MFS method in applications that allow any kind of time-independent magnetic field as the background component, no longer restricted to potential (current-free) settings. At the same time, we wish to also allow for resistive MHD applications that are aided by this more general MFS technique. The derivation of the governing equations employing an arbitrary split in a time-independent ${{\boldsymbol{B}}}_{0}$ are repeated below, to extend them further on to resistive MHD. The ideal MHD equations in conservative form are given by

$$\begin{eqnarray}&&\displaystyle \frac{\partial \rho }{\partial t}+{\rm{\nabla }}\cdot (\rho {\boldsymbol{v}})=0,\end{eqnarray} \tag{ 19 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {\boldsymbol{v}})}{\partial t}+{\rm{\nabla }}\cdot \left(\rho {\boldsymbol{vv}}+(p+\displaystyle \frac{{\boldsymbol{B}}\cdot {\boldsymbol{B}}}{2{\mu }_{0}}){\boldsymbol{I}}-\displaystyle \frac{{\boldsymbol{BB}}}{{\mu }_{0}}\right)=0,\end{eqnarray} \tag{ 20 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial E}{\partial t}+{\rm{\nabla }}\cdot \left(E{\boldsymbol{v}}+(p+\displaystyle \frac{{\boldsymbol{B}}\cdot {\boldsymbol{B}}}{2{\mu }_{0}}){\boldsymbol{v}}-\displaystyle \frac{{\boldsymbol{B}}}{{\mu }_{0}}({\boldsymbol{B}}\cdot {\boldsymbol{v}})\right)=0,\end{eqnarray} \tag{ 21 }$$

$$\begin{eqnarray}&&\displaystyle \frac{\partial {\boldsymbol{B}}}{\partial t}+{\rm{\nabla }}\cdot ({\boldsymbol{vB}}-{\boldsymbol{Bv}})=0,\end{eqnarray} \tag{ 22 }$$

where ρ, ${\boldsymbol{v}}$, ${\boldsymbol{B}}$, and ${\boldsymbol{I}}$ are the plasma density, velocity, magnetic field, and unit tensor, respectively. In solar applications, gas pressure is $p=2.3{n}_{{\rm{H}}}{k}_{{\rm{B}}}T$, assuming full ionization and a solar hydrogen to helium abundance ${n}_{\mathrm{He}}/{n}_{{\rm{H}}}=0.1$, where $\rho =1.4{n}_{{\rm{H}}}{m}_{p}$ (or the mean molecular weight $\tilde{\mu }\approx 0.6087$), while $E=p/(\gamma -1)+\rho {v}^{2}/2\,+\,{B}^{2}/2{\mu }_{0}$ is the total energy. Consider ${\boldsymbol{B}}={{\boldsymbol{B}}}_{0}+{{\boldsymbol{B}}}_{1}$, where ${{\boldsymbol{B}}}_{0}$ is a time-independent magnetic field, satisfying $\partial {{\boldsymbol{B}}}_{0}/\partial t=0$ and ${\rm{\nabla }}\cdot {{\boldsymbol{B}}}_{0}=0$. Equation (20) can be written as

$$\begin{eqnarray}&&\displaystyle \frac{\partial (\rho {\boldsymbol{v}})}{\partial t}+{\rm{\nabla }}\cdot \left(\rho {\boldsymbol{vv}}+(p+\displaystyle \frac{{B}_{1}^{2}}{2{\mu }_{0}}){\boldsymbol{I}}-\displaystyle \frac{{{\boldsymbol{B}}}_{1}{{\boldsymbol{B}}}_{1}}{{\mu }_{0}}\right)\\ &&\quad \quad \quad +{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1}}{{\mu }_{0}}{\boldsymbol{I}}-\displaystyle \frac{{{\boldsymbol{B}}}_{0}{{\boldsymbol{B}}}_{1}+{{\boldsymbol{B}}}_{1}{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}\right)\\ &&\quad \quad \quad =\displaystyle \frac{1}{{\mu }_{0}}({\rm{\nabla }}\times {{\boldsymbol{B}}}_{0})\times {{\boldsymbol{B}}}_{0}.\end{eqnarray} \tag{ 23 }$$

Defining ${E}_{1}\equiv p/(\gamma -1)+\rho {v}^{2}/2+{B}_{1}^{2}/(2{\mu }_{0})$, then $E={E}_{1}+({B}_{0}^{2}+2{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1})/(2{\mu }_{0})$ and Equation (21) can be written as

$$\begin{eqnarray}&&\displaystyle \frac{\partial {E}_{1}}{\partial t}+\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}\cdot \displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left({E}_{1}{\boldsymbol{v}}+\left(p+\displaystyle \frac{{B}_{1}^{2}}{2{\mu }_{0}}\right){\boldsymbol{v}}\right.\\ &&\quad \left.-\displaystyle \frac{{{\boldsymbol{B}}}_{1}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)+{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\quad +{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{B}}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{\boldsymbol{B}}}{{\mu }_{0}}({{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{v}})\right)=0.\end{eqnarray} \tag{ 24 }$$

When we take the scalar product of Equation (22) with a time-independent ${{\boldsymbol{B}}}_{0}$, we can use vector manipulations on the RHS of ${{\boldsymbol{B}}}_{0}\cdot \partial {{\boldsymbol{B}}}_{1}/\partial t={{\boldsymbol{B}}}_{0}\cdot {\rm{\nabla }}\times ({\boldsymbol{v}}\times {\boldsymbol{B}})$ to obtain

$$\begin{eqnarray}&&\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}\cdot \displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{B}}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{\boldsymbol{B}}}{{\mu }_{0}}({{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{v}})\right)\\ &&\quad =\,({\boldsymbol{v}}\times {\boldsymbol{B}})\cdot \displaystyle \frac{1}{{\mu }_{0}}{\rm{\nabla }}\times {{\boldsymbol{B}}}_{0}.\end{eqnarray} \tag{ 25 }$$

Inserting Equation (25) into Equation (24), we arrive at

$$\begin{eqnarray}&&\displaystyle \frac{\partial {E}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left({E}_{1}{\boldsymbol{v}}+\left(p+\displaystyle \frac{{B}_{1}^{2}}{2{\mu }_{0}}\right){\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{1}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\quad +{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\quad =\,-({\boldsymbol{v}}\times {\boldsymbol{B}})\cdot \displaystyle \frac{1}{{\mu }_{0}}{\rm{\nabla }}\times {{\boldsymbol{B}}}_{0}.\end{eqnarray} \tag{ 26 }$$

Therefore, in the ideal MHD system with MFS, we see how a source term appears in the RHS for the momentum Equation (23) that quantifies (partly) the Lorentz force ${{\boldsymbol{J}}}_{0}\times {{\boldsymbol{B}}}_{0}$, where ${{\boldsymbol{J}}}_{0}={\rm{\nabla }}\times {{\boldsymbol{B}}}_{0}/{\mu }_{0}$, while the energy Equation (26) for E₁ features a RHS written as ${\boldsymbol{E}}\cdot {{\boldsymbol{J}}}_{0}$ for the electric field ${\boldsymbol{E}}=-{\boldsymbol{v}}\times {\boldsymbol{B}}$. The induction equation, for a time-invariant ${{\boldsymbol{B}}}_{0}$ just writes as before:

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot ({{\boldsymbol{vB}}}_{1}-{{\boldsymbol{B}}}_{1}{\boldsymbol{v}})+{\rm{\nabla }}\cdot ({{\boldsymbol{vB}}}_{0}-{{\boldsymbol{B}}}_{0}{\boldsymbol{v}})=0.\end{eqnarray} \tag{ 27 }$$

For force-free magnetic fields, ${\rm{\nabla }}\times {{\boldsymbol{B}}}_{0}=\alpha {{\boldsymbol{B}}}_{0}$, where α is constant along one magnetic field line, we have ${{\boldsymbol{J}}}_{0}\times {{\boldsymbol{B}}}_{0}=0$ and $-({\boldsymbol{v}}\times {\boldsymbol{B}})\cdot {{\boldsymbol{J}}}_{0}=-({\boldsymbol{v}}\times {{\boldsymbol{B}}}_{1})\cdot {{\boldsymbol{J}}}_{0}$.

For resistive MHD, extra source terms ${\rm{\nabla }}\cdot ({\boldsymbol{B}}\times \eta {\boldsymbol{J}})/{\mu }_{0}$ and $-{\rm{\nabla }}\times (\eta {\boldsymbol{J}})$, are added on the RHS of the energy Equation (21) and the induction Equation (22), respectively, where ${\boldsymbol{J}}={\rm{\nabla }}\times {\boldsymbol{B}}/{\mu }_{0}$. Then the energy equation must account for Ohmic heating and magnetic field diffusion, to be written as

$$\begin{eqnarray}&&\displaystyle \frac{\partial {E}_{1}}{\partial t}+\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}\cdot \displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left({E}_{1}{\boldsymbol{v}}+\left(p+\displaystyle \frac{{B}_{1}^{2}}{2{\mu }_{0}}\right){\boldsymbol{v}}\right.\\ &&\left.\quad \quad -\displaystyle \frac{{{\boldsymbol{B}}}_{1}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)+{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\quad \quad +{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{B}}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{\boldsymbol{B}}}{{\mu }_{0}}({{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{v}})\right)=\eta {J}^{2}-\displaystyle \frac{1}{{\mu }_{0}}{{\boldsymbol{B}}}_{0}\cdot {\rm{\nabla }}\\ &&\quad \quad \times (\eta {\boldsymbol{J}})-\displaystyle \frac{1}{{\mu }_{0}}{{\boldsymbol{B}}}_{1}\cdot {\rm{\nabla }}\times (\eta {\boldsymbol{J}}).\end{eqnarray} \tag{ 28 }$$

The induction equation, extended with resistivity, now gives

$$\begin{eqnarray}&&\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}\cdot \displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{B}}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{\boldsymbol{B}}}{{\mu }_{0}}({{\boldsymbol{B}}}_{0}\cdot {\boldsymbol{v}})\right)\\ &&\quad =\,({\boldsymbol{v}}\times {\boldsymbol{B}})\cdot \displaystyle \frac{1}{{\mu }_{0}}{\rm{\nabla }}\times {{\boldsymbol{B}}}_{0}-\displaystyle \frac{1}{{\mu }_{0}}{{\boldsymbol{B}}}_{0}\cdot {\rm{\nabla }}\times (\eta {\boldsymbol{J}}).\end{eqnarray} \tag{ 29 }$$

Insert Equation (29) to Equation (28), and we have the resistive MHD energy equation in the MFS representation

$$\begin{eqnarray}&&\displaystyle \frac{\partial {E}_{1}}{\partial t}+{\rm{\nabla }}\cdot \left({E}_{1}{\boldsymbol{v}}+\left(p+\displaystyle \frac{{B}_{1}^{2}}{2{\mu }_{0}}\right){\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{1}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\,+\,{\rm{\nabla }}\cdot \left(\displaystyle \frac{{{\boldsymbol{B}}}_{0}\cdot {{\boldsymbol{B}}}_{1}}{{\mu }_{0}}{\boldsymbol{v}}-\displaystyle \frac{{{\boldsymbol{B}}}_{0}}{{\mu }_{0}}({{\boldsymbol{B}}}_{1}\cdot {\boldsymbol{v}})\right)\\ &&\quad =\,-({\boldsymbol{v}}\times {\boldsymbol{B}})\cdot {{\boldsymbol{J}}}_{0}+\eta {J}^{2}-\displaystyle \frac{1}{{\mu }_{0}}{{\boldsymbol{B}}}_{1}\cdot {\rm{\nabla }}\times (\eta {\boldsymbol{J}}).\end{eqnarray} \tag{ 30 }$$

The induction equation, as implemented, is then written as

$$\begin{eqnarray}&&\displaystyle \frac{\partial {{\boldsymbol{B}}}_{1}}{\partial t}+{\rm{\nabla }}\cdot ({{\boldsymbol{vB}}}_{1}-{{\boldsymbol{B}}}_{1}{\boldsymbol{v}})+{\rm{\nabla }}\cdot ({{\boldsymbol{vB}}}_{0}-{{\boldsymbol{B}}}_{0}{\boldsymbol{v}})\\ &&\quad =\,-{\rm{\nabla }}\times (\eta {\boldsymbol{J}}).\end{eqnarray} \tag{ 31 }$$

In the implementation of the MFS form of the MHD equations, we take the following strategies. Each time when creating a new block, a special user subroutine is called to calculate ${{\boldsymbol{B}}}_{0}$ at cell centers and cell interfaces which is stored in an allocated array, and then ${{\boldsymbol{J}}}_{0}$ is evaluated and stored at cell centers either numerically or analytically with an optional user subroutine. Note that when the block is deleted from the AMR mesh, these stored values are also lost. The third term on the LHS of the momentum Equation (23), energy Equation (26) or (28), and in the induction Equation (27) or (31) is added in the flux computation for the corresponding variable, based on pre-determined ${{\boldsymbol{B}}}_{0}$ magnetic field values at the cell interfaces where fluxes are evaluated. The terms on the RHS of all equations are treated as unsplit source terms, which are added in each sub-step of a time integration scheme. We use simple central differencing to evaluate spatial derivatives at cell centers. For example, to compute ${\rm{\nabla }}\times (\eta {\boldsymbol{J}})$ in the physical region of a block excluding ghost cells, we first compute ${{\boldsymbol{J}}}_{1}$ in a block region including the first layer of ghost cells, which needs ${{\boldsymbol{B}}}_{1}$ at the second layer of ghost cells.

We present three tests and one application to demonstrate the validity and advantage of the MFS technique. All three tests are solved with a finite-volume scheme setup combining the HLL solver (Harten et al. 1983) with Čada's compact third-order limiter (Čada & Torrilhon 2009) for reconstruction, and a three-step Runge–Kutta time integration in a dimensionally unsplit approach. We use a diffusive term in the induction equation to keep the divergence of magnetic field under control (Keppens et al. 2003; van der Holst & Keppens 2007; Xia et al. 2014). We adopt a constant index of $\gamma =5/3$. Unless stated explicitly, we employ dimensionless (code) units everywhere, also making ${\mu }_{0}=1$.

3.2.1. 3D Force-free Magnetic Flux Rope

This is a test initialized with a static plasma threaded by a force-free, straight helical magnetic flux rope on a Cartesian grid (see Figure 7). The initial density and gas pressure are uniformly set to unity. The simulation box has a size of 6 × 6 × 6 and is resolved by a $128\times 128\times 128$ uniform mesh which is decomposed into blocks of $16\times 16\times 16$ cells. The magnetic field is non-potential and nonlinearly force-free, as proposed by Low (1977), and is formulated as

$$\begin{eqnarray}{B}_{x} & = & \displaystyle \frac{4\xi }{1+{\xi }^{2}}f(y,z),{B}_{y}=2\left({kz}+\displaystyle \frac{1-{\xi }^{2}}{1+{\xi }^{2}}\right)f(y,z),\\ {B}_{z} & = & -2{kyf}(y,z),\end{eqnarray} \tag{ 32 }$$

$$\begin{eqnarray}&&f(y,z)={B}_{a}{\left[\displaystyle \frac{4{\xi }^{2}}{{(1+{\xi }^{2})}^{2}}+{k}^{2}{y}^{2}+{\left({kz}+\displaystyle \frac{1-{\xi }^{2}}{1+{\xi }^{2}}\right)}^{2}\right]}^{-1}.\end{eqnarray} \tag{ 33 }$$

We choose free parameters $\xi =1$ and k = 0.5 to make the axis of the flux rope align with the x-axis and set B_a = 10. The electric current of this flux rope is analytically found to be

$$\begin{eqnarray}{J}_{x} & = & 4{kf}(y,z)+4{{kB}}_{a}^{-1}f{(y,z)}^{2}\\ & & \times \left[{k}^{2}{y}^{2}+{\left({kz}+\displaystyle \frac{1-{\xi }^{2}}{1+{\xi }^{2}}\right)}^{2}\right],\\ {J}_{y} & = & \displaystyle \frac{8\xi k}{1+{\xi }^{2}}{B}_{a}^{-1}f{(y,z)}^{2}\left({kz}+\displaystyle \frac{1-{\xi }^{2}}{1+{\xi }^{2}}\right),\\ {J}_{z} & = & -\displaystyle \frac{8\xi k}{1+{\xi }^{2}}{B}_{a}^{-1}f{(y,z)}^{2}y.\end{eqnarray} \tag{ 34 }$$

The plasma β ranges from 0.006 to 0.027. The Alfvén crossing time along y-axis across the box is 0.377, determined by the averaged Alfvén speed along the y-axis. This analytical force-free static equilibrium should remain static forever. However, due to the finite numerical diffusion of the numerical scheme adopted, the current in the flux rope slowly dissipates when we do not employ the MFS strategy, thereby converting magnetic energy to internal energy and resulting in (small but) non-zero velocities. After 5 (dimensionless code) time units (about 8500 CFL limited timesteps), as shown in Figure 7, the reference run without MFS has up to 20% increase in temperature near the central axis of the flux rope, while the run with MFS perfectly maintains the initial temperature. Neither run has a discernible change in magnetic structure.

Zoom In Zoom Out Reset image size

We quantify the relative changes, $(f(t)-f(0))/f(0)$, of total magnetic energy, electric current, and internal energy in time for both runs and plot them in Figure 8. In the reference run without MFS, the magnetic energy decreases up to 0.02%, current decreases 0.15%, and internal energy increases 1.8% at 5 time units. Thus, the dissipation of magnetic energy and current and the resulting increase of internal energy with the employed discretization are significant for long-term runs. However, the run with the MFS strategy keeps the initial equilibrium perfectly and all relative changes are exactly zero.

Zoom In Zoom Out Reset image size

3.2.2. 2D Non-potential Magnetic Null-point

This second test focuses on using the MFS technique in a setup where a magnetic null point is present (where magnetic field locally vanishes) in a 2D planar configuration. Using a magnetic vector potential ${\boldsymbol{A}}=[0,0,{A}_{z}]$ with ${A}_{z}=0.25{B}_{c}[{({j}_{t}-{j}_{z}){(y-{y}_{c})}^{2}-({j}_{t}+{j}_{z})(x-{x}_{c})}^{2}]$, the resulting magnetic field works out to

$$\begin{eqnarray}{B}_{x} & = & 0.5{B}_{c}({j}_{t}-{j}_{z})(y-{y}_{c}),\\ {B}_{y} & = & 0.5{B}_{c}({j}_{t}+{j}_{z})(x-{x}_{c}),{B}_{z}=0.\end{eqnarray} \tag{ 35 }$$

Its current density is

$$\begin{eqnarray}&&{J}_{x}={J}_{y}=0,{J}_{z}={B}_{c}{j}_{z}.\end{eqnarray} \tag{ 36 }$$

This magnetic field has a 2D non-potential null-point in the middle, as seen in the magnetic field lines shown in the left panel of Figure 9. The domain has $x\in [-0.5,0.5]$ and $y\in [0,2]$ and is resolved by a uniform mesh of 128 × 256 cells. We take x_c = 0 and y_c = 1 to make the null point appear at the center of the domain. To achieve a static equilibrium, the non-zero Lorentz force is balanced by a pressure gradient force as

$$\begin{eqnarray}&&{\boldsymbol{J}}\times {\boldsymbol{B}}-{\rm{\nabla }}p=0.\end{eqnarray} \tag{ 37 }$$

By solving this, we have the gas pressure as $p(x,y)={B}_{c}{j}_{z}{A}_{z}+{p}_{0}$. The initial density is uniformly 1, and all is static. The arrows in the right panel of Figure 9 only show the direction of the Lorentz force. We choose dimensionless values of B_c = 10, ${p}_{0}=7$, j_t = 2.5, and j_z = 1. The Alfvén crossing time along the y-axis across the box is about 1. Plasma β ranges from 0.06 at the four corners to 8782 near the null point. To test how well the numerical solver maintains this initial static equilibrium, we perform runs with or without MFS. All variables except for velocity are fixed as their initial values in all boundaries, and velocity is made anti-symmetric about boundary surfaces to ensure zero velocity at all boundaries.

Zoom In Zoom Out Reset image size

After 10 time units (about 22,550 CFL limited time steps) in the MFS run, the density decreases at most 0.038% in the central horizontal line near the side boundaries and increases 0.02% in the central vertical line as shown in Figure 9, which corresponds to numerically generated diverging and converging flows to the horizontal and vertical line, respectively, with very small speeds of magnitude at most 2 × 10⁻⁴, which is only a 6 × 10⁻³ fraction of the local Alfvén speed. This cross-shaped pattern has only four cells in width. The reference run without MFS gives almost the same images as in Figure 9. The MFS run splits off the entire field above as ${{\boldsymbol{B}}}_{0}$ with its non-zero Lorentz force, and gives essentially the same results as the standard solver for the equilibrium state. We then perform a convergence study with increasing grid resolution, and plot kinetic energy, the ratio between kinetic energy and total energy, and magnetic energy normalized by its initial value at 10 time units in Figure 10. Both MFS runs and reference runs without MFS present very similar converging behavior and errors (deviations from the initial equilibrium) decrease with increasing resolution at fifthth order of accuracy. Therefore the correctness of the MFS technique for non-force-free fields is justified.

Zoom In Zoom Out Reset image size

3.2.3. Current Sheet Diffusion

To test the MFS technique in resistive MHD, we first test dissipation of a straight current sheet with uniform resistivity. The magnetic field changes direction smoothly in the current sheet located at x = 0 as given by

$$\begin{eqnarray}&&{B}_{x}=0,\,{B}_{y}=-{B}_{d}\tanh ({c}_{w}x),\,{B}_{z}={B}_{d}/\cosh ({c}_{w}x).\end{eqnarray} \tag{ 38 }$$

Its current density is

$$\begin{eqnarray}{J}_{x} & = & 0,{J}_{y}=5{B}_{d}\tanh ({c}_{w}x)/\cosh ({c}_{w}x),\\ {J}_{z} & = & -5{B}_{d}/{\cosh }^{2}({c}_{w}x).\end{eqnarray} \tag{ 39 }$$

In this test, we adopt parameter values B_d = 4 and current sheet width c_w = 5. It is a nonlinear force-free field from a previous numerical study of magnetic reconnection of solar flares (Yokoyama & Shibata 2001). Initial density and gas pressure are uniformly 1.

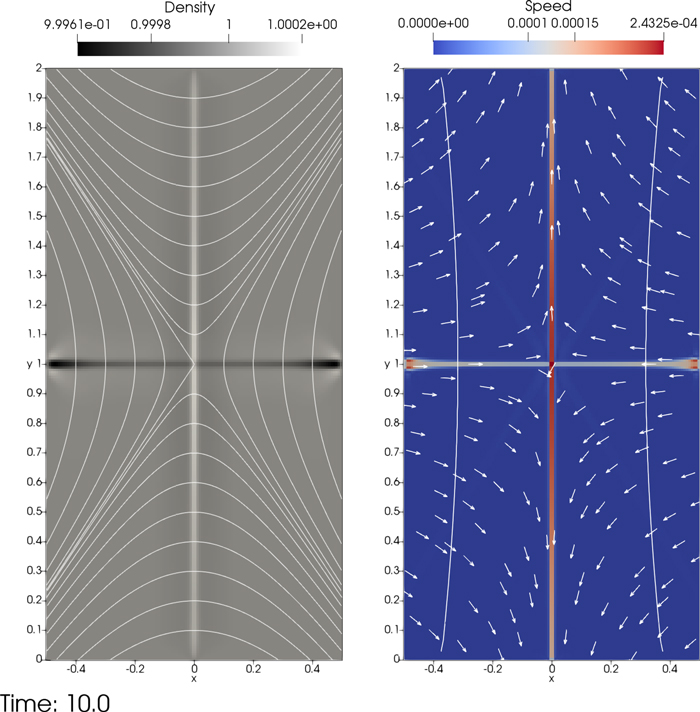
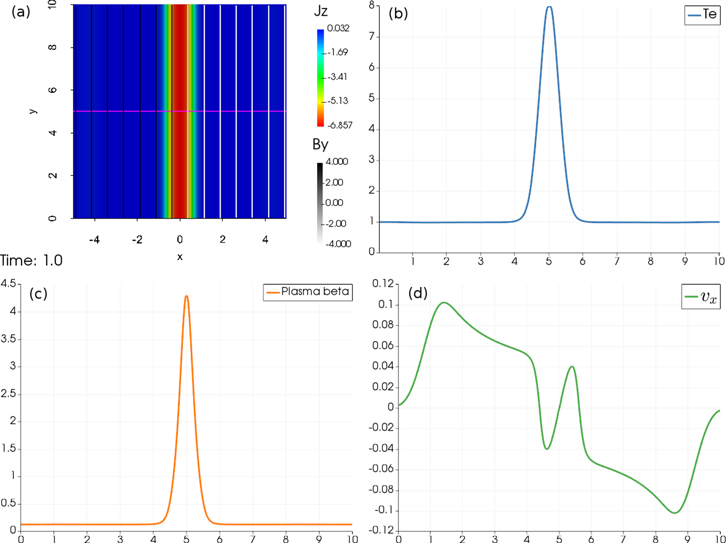
We adopt a constant resistivity η with a dimensionless value of 0.1. The simulation box is 10 × 10 discretized on a four-level AMR mesh with an effective resolution of 512 × 512 cells. The average Alfvén crossing time is 2.5. After 1 time unit in an MFS run, the current is dissipated due to the resistivity as shown in panel (a) from Figure 11, presenting the z-component of current in rainbow color and magnetic field lines in gray scale. The Ohmic heating increases the temperature in the current sheet from 1 to 8, as shown in panel (b), with flows toward the current sheet from outside and velocity pointing outward in the heated current sheet as shown in panel (d). Plasma β ranges from 0.125 outside the current sheet and 4.2 in the middle of the current sheet. The reference run without MFS gives indistinguishable images as in Figure 11. To exactly compare the two runs, we evaluated the time evolution of magnetic energy, internal energy, and electric current and plot them in circles for MFS run and in triangles for the reference run in Figure 12. The results for the two runs almost overlap and the decrease of magnetic energy corresponds well to the increase of internal energy, this time by means of the adopted physical dissipation. We plot the normalized difference between them in the bottom panel, where within 0.1% differences are found for all three quantities. Therefore, the correctness of the MFS technique for resistive MHD is verified.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

3.2.4. Solar Flare Application with Anomalous Resistivity

To show the advantage of the MFS technique in fully resistive settings, we present its application on a magnetic reconnection test which extends the simulations of solar flares by Yokoyama & Shibata (2001) to extremely low-β, more realistic situations. Here, a run without the MFS technique using our standard MHD solver fails due to negative pressure.

We set up the simulation box in $x\in [-10,10]$ and $y\in [0,20]$ with a four-level AMR mesh, which has an effective resolution of 2048 × 2048 and smallest cell size of 97 km. The magnetic field setup is the same current sheet as before, and follows Equation (38) with parameters B_d = 50 and c_w = 6.667. Now, a 2D setup is realized with vertically varying initial density and temperature profiles as in Yokoyama & Shibata (2001), where a hyperbolic tangent function was used to smoothly connect a corona region with a high-density chromosphere. By neglecting solar gravity and setting constant gas pressure everywhere, the initial state is in an equilibrium. The current sheet is then first perturbed by an anomalous resistivity ${\eta }_{1}$ in a small circular region in the current sheet when time $t\lt 0.4$, and afterwards the anomalous resistivity ${\eta }_{2}$ is switched to a more physics-based value depending on the relative ion–electron drift velocity. The formula of anomalous resistivity ${\eta }_{1}$ is

$$\begin{eqnarray}{\eta }_{1}=\left\{\begin{array}{ll}{\eta }_{c}[2{(r/{r}_{\eta })}^{3}-3{(r/{r}_{\eta })}^{2}+1] & \mathrm{if}\ r\leqslant {r}_{\eta },\\ 0 & \mathrm{if}\ r\gt {r}_{\eta },\end{array}\right.\end{eqnarray} \tag{ 40 }$$

where ${\eta }_{c}=0.002$ is the amplitude, $r=\sqrt{{x}^{2}+{(y-6)}^{2}}$ is the distance from the center of the spot at $(x=0,y=6)$, and ${r}_{\eta }=0.24$ is the radius of the spot. The formula of anomalous resistivity ${\eta }_{2}$ is

$$\begin{eqnarray}{\eta }_{2}=\left\{\begin{array}{ll}0 & \mathrm{if}\ {v}_{d}\lt {v}_{c},\\ {\alpha }_{\eta }({v}_{d}/{v}_{c}-1) & \mathrm{if}\ {v}_{d}\geqslant {v}_{c}.\end{array}\right.\end{eqnarray} \tag{ 41 }$$

where ${v}_{d}=\sqrt{{J}_{x}^{2}+{J}_{y}^{2}+{J}_{z}^{2}}/({en})$ is the relative ion–electron drift velocity (e is the electric charge of the electron and n is number density of the plasma), ${v}_{c}=5\times {10}^{-5}$ is the threshold of the anomalous resistivity, and ${\alpha }_{\eta }=4\times {10}^{-3}$ is the amplitude.

Continuous boundary conditions are applied for all boundaries and all variables except that B_x = 0 and zero velocity is imposed at the bottom boundary. We basically adopt the same setup and physical parameters as in Yokoyama & Shibata (2001), except that the magnitude of the magnetic field here reaches 100 G with plasma β of 0.005, compared to about 76 G and 0.03 in the original work. We use normalization units of length L_u = 10 Mm, time ${t}_{u}=85.87\,{\rm{s}}$, temperature ${T}_{u}={10}^{6}$ K, number density ${n}_{u}={10}^{9}$ cm⁻³, velocity v_u = 116.45 km s⁻¹, and magnetic field B_u = 2 G. Since we use different normalization units to normalize the same physical parameters, our dimensionless values are different from Yokoyama & Shibata's work. We choose a scheme combining HLL flux with van Leer's slope limiter (van Leer 1974) and two-step time integration. Powell's eight-wave method (Powell et al. 1999) is used to clean divergence of the magnetic field. Thermal conduction along magnetic field lines is solved using techniques that are described in detail in Section 4.

Inspired by Figure 3 in Yokoyama & Shibata (2001), we show very similar results in Figure 13, which presents snapshots of the density and temperature distribution at times 0.5, 0.64, and 0.75. The temporal evolution of the magnetic reconnection process and the evaporation in flare loops are reproduced. Flow directions and magnetic field lines are also plotted. Magnetic reconnection starts at the center x = 0, y = 6 of the enhanced resistive region, where an X-point is formed. Reconnected field lines with heated plasma are continuously ejected from the X-point to the positive and negative y-directions because of the tension force of the reconnected field lines.

Zoom In Zoom Out Reset image size

To solve the thermal conduction Equation (42), various numerical schemes based on centered differencing have been developed. The simplest example is to evaluate gradients directly with second-order central differencing; more advanced methods include the asymmetric scheme described in Günter et al. (2005) and Parrish & Stone (2005) and the symmetric scheme of Günter et al. (2005). However, these schemes can cause heat to flow from low to high temperature if there are strong temperature gradients (Sharma & Hammett 2007), which is unphysical.

To understand why such effects can occur, consider Equation (42). Suppose a finite-volume discretization is used in 2D, and that we want to compute the heat flux in the x-direction at the cell interface between cell (i,j) and $(i+1,j)$. The term $({\kappa }_{\parallel }-{\kappa }_{\perp })({\boldsymbol{b}}\cdot {\rm{\nabla }}T){\boldsymbol{b}}$ is then given by $({\kappa }_{\parallel }-{\kappa }_{\perp })({b}_{x}^{2}{\partial }_{x}T+{b}_{x}{b}_{y}{\partial }_{y}T)$. The term ${b}_{x}^{2}{\partial }_{x}T$ will always be heat flux transported from hot to cold. When ${b}_{x}{b}_{y}{\partial }_{y}T$ has the opposite sign of ${b}_{x}^{2}{\partial }_{x}T$ and a larger magnitude, a resulting unphysical heat flux from cold to hot occurs.

Avoiding the above problem, which can lead to negative temperatures, is especially important for astrophysical plasmas with sharp temperature gradients. Examples are the transition region in the solar corona separating the hot corona and the cool chromosphere, or the disk–corona interface in accretion disks. A solution was proposed in Sharma & Hammett (2007), in which slope limiters were applied to the transverse component of the heat flux. Since the slope-limited symmetric scheme was found to be less diffusive than the limited asymmetric scheme, we follow Sharma & Hammett (2007) and implement it in our code, with the extra extension to (temperature-dependent) Spitzer conductivity and generalized to a 3D setup in Cartesian coordinates. The explicit, conservative finite difference formulation of Equation (42) is then

$$\begin{eqnarray}&&{e}_{i,j,k}^{n+1}={e}_{i,j,k}^{n}+{\rm{\Delta }}t\left(\displaystyle \frac{{q}_{x,i+1/2,j,k}^{n}-{q}_{x,i-1/2,j,k}^{n}}{{\rm{\Delta }}x}+\right.\end{eqnarray} \tag{ 44 }$$

$$\begin{eqnarray}&&\left.\displaystyle \frac{{q}_{y,i,j+1/2,k}^{n}-{q}_{y,i,j-1/2,k}^{n}}{{\rm{\Delta }}y}+\displaystyle \frac{{q}_{z,i,j,k+1/2}^{n}-{q}_{y,i,j,k-1/2}^{n}}{{\rm{\Delta }}z}\right),\end{eqnarray} \tag{ 45 }$$

involving face-centered evaluations of heat flux, e.g. along the x-coordinate, given by

$$\begin{eqnarray}&&{q}_{x}=\kappa {b}_{x}\left({b}_{x}\displaystyle \frac{\partial T}{\partial x}+{b}_{y}\displaystyle \frac{\partial T}{\partial y}+{b}_{z}\displaystyle \frac{\partial T}{\partial z}\right)+{\kappa }_{\perp }\displaystyle \frac{\partial T}{\partial x},\end{eqnarray} \tag{ 46 }$$

in which $\kappa ={\kappa }_{\parallel }-{\kappa }_{\perp }$.

Since we use an explicit scheme for time integration, the time step ${\rm{\Delta }}t$ must satisfy the condition for numerical stability:

$$\begin{eqnarray}&&{\rm{\Delta }}t\leqslant {c}_{p}\min \left(\displaystyle \frac{\rho {\rm{\Delta }}{x}^{2}}{(\gamma -1){\kappa }_{\parallel }{b}_{x}^{2}},\displaystyle \frac{\rho {\rm{\Delta }}{y}^{2}}{(\gamma -1){\kappa }_{\parallel }{b}_{y}^{2}},\displaystyle \frac{\rho {\rm{\Delta }}{z}^{2}}{(\gamma -1){\kappa }_{\parallel }{b}_{z}^{2}}\right),\end{eqnarray} \tag{ 47 }$$

where c_p is a stability constant taking value of 0.5 and 1/3 for 2D and 3D, respectively. With increasing grid resolution and/or high thermal conductivity, this limit on ${\rm{\Delta }}t$ can be much smaller than the CFL time step limit for solving the ideal MHD equations explicitly. Therefore multiple steps of solving thermal conduction within one-step MHD evolution are suggested to alleviate the time step restriction from thermal conduction. In our actual solar coronal applications, we adopt a super-timestepping RKL2 scheme proposed by Meyer et al. (2012), where every parabolic update uses an s-stage Runge–Kutta scheme with s and its coefficients determined in accord with the two-term recursion formula for Legendre polynomials. In what follows, we just concentrate on the details to handle a single step for the thermal conduction update.

The first term on the RHS of expression (46) is discretized as the limited face-centered heat flux:

$$\begin{eqnarray}&&{q}_{{xx},i+1/2,j,k}={\kappa }_{i+1/2,j,k}{\left(\overline{{b}_{x}^{2}\displaystyle \frac{\partial T}{\partial x}}\right)}_{i+1/2,j,k},\end{eqnarray} \tag{ 48 }$$

where the local thermal conduction coefficient is found by first quantifying its value at the cell corners, in 3D (${n}_{{\rm{D}}}=3$) found from

$$\begin{eqnarray}&&{\kappa }_{i+1/2,j+1/2,k+1/2}=\displaystyle \frac{1}{{2}^{{n}_{{\rm{D}}}}}\displaystyle \sum _{n=0}^{1}\displaystyle \sum _{m=0}^{1}\displaystyle \sum _{l=0}^{1}{\kappa }_{i+l,j+m,k+n},\end{eqnarray} \tag{ 49 }$$

to then derive the face-centered values as in

$$\begin{eqnarray}&&{\kappa }_{i+1/2,j,k}=\displaystyle \frac{1}{{2}^{{n}_{{\rm{D}}}-1}}\displaystyle \sum _{n=0}^{1}\displaystyle \sum _{m=0}^{1}{\kappa }_{i+1/2,j+1/2-m,k+1/2-n}.\end{eqnarray} \tag{ 50 }$$

The face-centered, limited flux expression is given by

$$\begin{eqnarray}{\left(\overline{{b}_{x}^{2}\displaystyle \frac{\partial T}{\partial x}}\right)}_{i+1/2,j,k} & = & \displaystyle \frac{1}{{2}^{{n}_{{\rm{D}}}-1}}\displaystyle \sum _{n=0}^{1}\displaystyle \sum _{m=0}^{1}\\ & & \times {\left({b}_{x}^{2}\widetilde{\displaystyle \frac{\partial T}{\partial x}}\right)}_{i+1/2,j+1/2-m,k+1/2-n},\end{eqnarray} \tag{ 51 }$$

in which corner values for the magnetic field aligned unit vectors are found as in

$$\begin{eqnarray}&&{b}_{x,i+1/2,j+1/2,k+1/2}=\displaystyle \frac{1}{{2}^{{n}_{{\rm{D}}}}}\displaystyle \sum _{n=0}^{1}\displaystyle \sum _{m=0}^{1}\displaystyle \sum _{l=0}^{1}{b}_{x,i+l,j+m,k+n},\end{eqnarray} \tag{ 52 }$$

while the limited temperature gradient in cell corners is found from

$$\begin{eqnarray}&&{\left.\widetilde{\displaystyle \frac{\partial T}{\partial x}}\right|}_{i+1/2,j+1/2-m,k+1/2-n}\\ =\,\left\{\begin{array}{ll}\bar{q} & \mathrm{if}\ \min q\lt \bar{q}\lt \max q,\\ \min q & \mathrm{if}\ \bar{q}\leqslant \min q,\\ \max q & \mathrm{if}\ \bar{q}\geqslant \max q,\end{array}\right.\end{eqnarray} \tag{ 53 }$$

$$\begin{eqnarray}&&\mathrm{where}\ \bar{q}={\left.\overline{\displaystyle \frac{\partial T}{\partial x}}\right|}_{i+1/2,j+1/2-m,k+1/2-n},\end{eqnarray} \tag{ 54 }$$

$$\begin{eqnarray}&&{\left.\overline{\displaystyle \frac{\partial T}{\partial x}}\right|}_{i+1/2,j+1/2,k+1/2}=\displaystyle \frac{1}{{2}^{{n}_{{\rm{D}}}-1}}\displaystyle \sum _{a=0}^{1}\displaystyle \sum _{b=0}^{1}{\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j+a,k+b},\end{eqnarray} \tag{ 55 }$$

$$\begin{eqnarray}&&\min q=\min \left(\alpha {\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j,k},1/\alpha {\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j,k}\right),\end{eqnarray} \tag{ 56 }$$

$$\begin{eqnarray}&&\max q=\max \left(\alpha {\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j,k},1/\alpha {\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j,k}\right),\end{eqnarray} \tag{ 57 }$$

$$\begin{eqnarray}&&\mathrm{and}\ \mathrm{finally}\ {\left.\displaystyle \frac{\partial T}{\partial x}\right|}_{i+1/2,j,k}=({T}_{i+1,j,k}-{T}_{i,j,k})/{\rm{\Delta }}x.\end{eqnarray} \tag{ 58 }$$

Similar formulae (involving fewer summations in the averaging) apply at lower dimensionality ${n}_{{\rm{D}}}$. We choose $\alpha =0.75$ for 2D runs, the same value as used by Sharma & Hammett (2007), and $\alpha =0.85$ for 3D runs to achieve least numerical diffusion according to our trial-and-error numerical tests. Note that in our code, as assumed in the above, the magnetic field components (and other quantities, like temperature) are defined at cell centers, and different formulae would be needed for a staggered grid where magnetic field is defined at cell faces, such as commonly adopted in constrained transport schemes.

The second and third terms of Equation (46) are transverse components q_xy and q_xz of heat conduction; we illustrate the discretization of the second term here and the third term can be derived similarly:

$$\begin{eqnarray}&&{q}_{{xy},i+1/2,j,k}={\kappa }_{i+1/2,j,k}{\left({b}_{x}{b}_{y}\overline{\displaystyle \frac{\partial T}{\partial y}}\right)}_{i+1/2,j,k},\end{eqnarray} \tag{ 59 }$$

where ${b}_{x,i+1/2,j,k}=0.5({b}_{x,i,j,k}+{b}_{x,i+1,j,k})$ and ${b}_{y,i+1/2,j,k}$ follow the same formula as Equation (50) for ${\kappa }_{i+1/2,j,k}$. The limited, face-centered temperature gradient is evaluated as in

$$\begin{eqnarray}&&{\left.\overline{\displaystyle \frac{\partial T}{\partial y}}\right|}_{i+1/2,j,k}=L\left({\left.\displaystyle \frac{\partial T}{\partial y}\right|}_{i,j,k}^{L},{\left.\displaystyle \frac{\partial T}{\partial y}\right|}_{i+1,j,k}^{L}\right)\end{eqnarray} \tag{ 60 }$$

in which

$$\begin{eqnarray}&&{\left.\displaystyle \frac{\partial T}{\partial y}\right|}_{i,j,k}^{L}=L\left({\left.\displaystyle \frac{\partial T}{\partial y}\right|}_{i,j+1/2,k},{\left.\displaystyle \frac{\partial T}{\partial y}\right|}_{i,j-1/2,k}\right)\end{eqnarray} \tag{ 61 }$$

where $L(a,b)$ is the monotonized central (MC) slope limiter, which is given by

$$\begin{eqnarray}\mathrm{MC}(a,b) & = & 2\mathrm{sign}(a)\max \{0,\min [| a| ,\mathrm{sign}(a)b,\\ & & \times \,\mathrm{sign}(a)(a+b)/4]\}.\end{eqnarray} \tag{ 62 }$$

We have tried other slope limiters such as minmod, vanleer, and superbee, but MC limiter gives the best results.

The last term of Equation (46) contributes to perpendicular thermal conduction and its discretized form computes the averaged face value of ${\kappa }_{\perp ,i+1/2,j,k}$ using the same form as Equation (50) and the averaged face value of the temperature gradient along x as in Equation (51) (and the equations that follow it), but without the factors b_x².

Since thermal conduction in dilute plasmas is caused by the movement of electrons, a larger thermal conduction flux implies faster electrons. Once the electron speed becomes comparable to the sound speed, plasma instabilities prevent the electrons from flowing faster and thermal conduction must saturate (Cowie & McKee 1977). We adopt the following formula from Cowie & McKee (1977) for a saturated thermal flux:

$$\begin{eqnarray}&&{q}_{\mathrm{sat}}=5\phi \rho {c}_{\mathrm{iso}}^{3},\end{eqnarray} \tag{ 63 }$$

where ${c}_{\mathrm{iso}}$ is the isothermal sound speed and the factor $\phi =1.1$ when the electron and ion temperatures are equal. We evaluate the projected saturated thermal flux at each cell face based on the averaged density and temperature there, and set it as the upper limit for the total thermal flux through that cell face, namely, $| {q}_{x,i+1/2,j,k}| \leqslant {q}_{\mathrm{sat},i+1/2,j,k}| {b}_{x,i+1/2,j,k}|$.

We implement the methods mentioned above in a thermal conduction module with source code written in the dimension-independent LASY way. Thus the same compact source code can be translated to pure Fortran code in 1D, 2D, or 3D before compilation.

A 2D circular ring diffusion test problem was proposed by Parrish & Stone (2005) and became a standard test for anisotropic thermal conduction (Sharma & Hammett 2007; Meyer et al. 2012). It initializes a hot patch in circular magnetic field lines in a $[-1,1]\times [-1,1]$ Cartesian box with temperatures

$$\begin{eqnarray}T=\left\{\begin{array}{ll}12 & \mathrm{if}\ 0.5\lt r\lt 0.7\ \mathrm{and}\ \displaystyle \frac{11}{12}\pi \lt \theta \lt \displaystyle \frac{13}{12}\pi ,\\ 10 & \mathrm{otherwise},\end{array}\right.\end{eqnarray} \tag{ 64 }$$

where $r=\sqrt{{x}^{2}+{y}^{2}}$ and $\tan \theta =y/x$. Density is set to 1. We create circular magnetic field lines centered at the origin by the formula:

$$\begin{eqnarray}&&{B}_{x}={10}^{-5}\cos (\theta +\pi /2)/r,\,\,\,{B}_{y}={10}^{-5}\sin (\theta +\pi /2)/r,\end{eqnarray} \tag{ 65 }$$

which is generated by an infinite line current perpendicular to the plane through the origin. The parallel thermal conductivity is constant and set to ${\kappa }_{\parallel }=0.01$ and no explicit perpendicular thermal conduction is considered. Continuous boundary conditions are used for all variable at all boundaries. We only evolve the anisotropic thermal heat conduction equation without solving the MHD equations, until 400 time units. Ideally, the diffusion of temperature should only occur in a ring $0.5\lt r\lt 0.7$ and eventually result in a uniform temperature of 10.1667 inside the ring with unperturbed temperature of 10 outside the ring. But perpendicular numerical diffusion may cause some cross-field thermal conduction and can smooth sharp temperature gradients at the borders of this ring.

The end state of a run (a) on a uniform 200 × 200 grid is shown in Figure 14(a). Temperature is high and nearly uniform inside the ring, with a constant background temperature of 10. The maximal and minimal temperature of the end state are 10.1687 and 10, respectively. No temperature overshooting is found near sharp temperature gradient regions and the monotonicity property is preserved. The final temperature distribution agrees with previous findings (see the fourth panel in Figure 6 of Sharma & Hammett 2007). Since the exact solution of this problem is a uniform temperature of 10.1667 in the ring and 10 outside it, we can evaluate the L₁, L₂, and ${L}_{\infty }$ norm errors for four runs with increasing resolution (see Table 1). The L₁ norm converges with a rate of 1.4 and the L₂ norm converges with a rate of 0.8. The maximal temperature is getting closer to the correct solution with increasing resolution and the minimal temperature stays at the correct value of 10. A rough estimate for the time-averaged perpendicular numerical diffusion (conductivity) ${\kappa }_{\perp ,\mathrm{num}}$ and its ratio to ${\kappa }_{\parallel }=0.01$ are calculated following the same method as in Sharma & Hammett (2007), and reported in the last column of Table 1. Note in particular that we can get this ratio from order 10⁻³ down to order 10⁻⁵ on sufficiently large grids, so that we can add physical perpendicular thermal conduction coefficients that exceed these values.

Zoom In Zoom Out Reset image size

Table 1.  Accuracy Measures of the Ring Diffusion Tests on Uniform Grids

Resolution	L1 error	L2 error	${L}_{\infty }$ error	${T}_{\max }$	${T}_{\min }$	${\kappa }_{\perp ,\mathrm{num}}/{\kappa }_{\parallel }$
50 × 50	0.03037	0.04705	0.08617	10.0842	10	$4.345\times {10}^{-3}$
100 × 100	0.01338	0.02704	0.11654	10.1355	10	$5.145\times {10}^{-4}$
200 × 200	0.00521	0.01592	0.08683	10.1663	10	$1.050\times {10}^{-4}$
400 × 400	0.00320	0.01224	0.08758	10.1681	10	$3.353\times {10}^{-5}$

Download table as:  ASCIITypeset image

In order to use the thermal conduction on an AMR grid, refluxing operations are needed to ensure flux conservation across fine–coarse interfaces. We store the thermal fluxes of blocks with finer or coarser neighbor blocks, and send thermal fluxes at fine–coarse interfaces from finer blocks to coarser blocks. This is standard practice for ensuring conservation in finite-volume AMR computations, and our strategy in terms of parallel communication patterns involved is found in Section 3.4 of Keppens et al. (2012). Figure 14(b) shows the end state of run (b) on an AMR grid with three levels and an effective resolution of 200 × 200. We use dynamic AMR, with the refine-triggering based on total energy using a Löhner type estimator (Lohner 1987; Keppens et al. 2012) and set a refine threshold of 0.08. Comparing to the result of the run in panel (a) on a uniform grid with the same resolution, run (b) gives comparable results. The AMR advantage is in the fact that it uses about 20% less computational time. Some minor quality degeneracy is present, with less sharp borders of the ring segment at the far end from the initial hot segment and a lower maximal temperature of 10.1638. This is likely caused by the larger numerical diffusion associated with the coarser grids at the far end. To prove the importance of the conservation fix, we show a run (d) with the same setup as run (b), except that it has no conservation fix, which ends up with lower temperature in the ring and stronger diffusion at its borders, as shown in Figure 14(d). To test our implementation of perpendicular thermal conduction, we perform test run (c) with a constant ${\kappa }_{\perp }=5\times {10}^{-5}=5\times {10}^{-3}{\kappa }_{\parallel }$ and other setups the same as run (a). As shown in Figure 14(c), the parallel thermal conduction dominates the diffusion of initial temperature pattern while finite perpendicular thermal conduction significantly smoothed the hot ring pattern in the radial direction of the ring perpendicular to magnetic field lines, comparing to run (a). The test run (c) demonstrates the correctness of our implementation of perpendicular thermal conduction, which may become non-negligible in plasma with very weak magnetic field.

We generalize the 2D ring diffusion test to a 3D version. In a 3D ${[-1,1]}^{3}$ Cartesian box, we rotate the magnetic field loops, from a position at first in the x–y plane, around the x-axis 45°, and then rotate around the z-axis 45°, to make the magnetic field direction misaligned with the coordinates. Therefore, the thermal flux along magnetic field lines must include contributions from all three dimensions. An initial 3D hot patch is set to have the same extension in the plane of the magnetic loop as in the 2D case and an extension of 0.4 in the direction perpendicular to this plane. We run the test on a uniform $200\times 200\times 200$ mesh until 400 time units. As shown in Figure 15(a), the 3D isosurface of temperature at 10.16 represents a ring shape. A slice through the middle plane of the ring structure is shown in a warped view and colored by temperature in Figure 15(b), and is comparable with the previous 2D results. The maximal temperature in the hot ring of the slice is 10.1774 and its thickness is 10% larger than in the corresponding 2D tests. A translucent slice cutting through the ring in panel (a) shows, in panel (c), that its cross section has a rounded square shape, which is caused by large numerical diffusion at its corner edges. To test the 3D thermal conduction on an AMR mesh, we run the same 3D test problem on a three-level AMR mesh with base-level resolution of $50\times 50\times 50$, which has the same effective resolution as the previous test on a uniform mesh. The result is very similar to the uniform-mesh version with maximal temperature of 10.1727, while the run consumes 45% less computational time than the uniform-mesh run.

Zoom In Zoom Out Reset image size

To check the consistency between the 3D implementation and the 2D one, we set up a test of 2D ring diffusion problem in a 3D simulation. We set the magnetic field loops in the x–y plane and the initial hot patch has the same extension in the x and y directions as in the 2D setup and extends uniformly through the box in the z direction. Periodic boundary conditions are used at z boundaries and continuous boundary conditions are adopted at x and y boundaries. The simulation box has a size of 1 × 1 by 0.1 on a $200\times 200\times 20$ mesh. The temperature distribution is invariant in the z direction and its x–y plane slice is very close to the 2D result with the same resolution at 400 time units. The maximum and miminum temperatures are the same. The temperature transition region is about 4% broader in the 3D run. Therefore, the 3D implementation is consistent with the 2D one.

MPI-AMRVAC is written in Fortran extended by the LASY syntax (Tóth 1997). After source files have been translated by a LASY preprocessor, they can be compiled by a standard Fortran compiler. The main goal of the LASY syntax is to be able to write dimension-independent code. However, the LASY syntax was also used, for example, to:

• 1.  
  (optionally) include other source files,
• 2.  
  perform vectorization (e.g., loop over components),
• 3.  
  define parameters for specific applications,
• 4.  
  turn parts of the code on or off.

This extended use of the preprocessor made it harder to understand the code, especially as more and more features were added. The preprocessor in MPI-AMRVAC 2.0 has therefore been simplified; the only flags it now supports relate to the dimensionality of the problem. Hence, the preprocessor is now only used to translate dimension-independent code to 1D, 2D, or 3D. This simplification of the preprocessor also required another modernization: instead of source files that were optionally included as flags were turned on or off, we now make use of standard Fortran modules. This made it possible to compile the full framework into a static library, including all the physics modules at once. This helps to ensure code stays compatible (and compiles) whenever changes are made, and significantly reduces compilation times. Furthermore, parallel compilation is now supported.

The modifications imply that the user program now has to specify which type of major physics module to activate, for example the hydrodynamics or MHD one (previously handled through the preprocessor and before compilation). As all modules are now available in the library version, this raises awareness of users to the full framework functionality, and each physics module now comes with its own settings and parameters, for example whether or not an energy equation should be used, or how many tracers (or dust species in coupled gas-dust hydro problems) to be included. Thanks to that, users can switch on/off special functionalities, like thermal conduction, radial stretching grid, particles etc., by just choosing appropriate parameters in an input parameter file without wasting time on recompilation, which was needed more frequently in the old code. Furthermore, we provide extensive support for customization to a large variety of applications by using function pointers. A user has to provide a routine for setting initial conditions, but can also specify custom routines for boundary conditions, additional source terms, custom output routines etc. There have also been many smaller changes to help users, most importantly those related to handling the coordinate system explicitly (by selecting, e.g., Cartesian 2D or 2.5D, or cylindrical, polar up to spherical 3D). Methods are encoded to automatically use the right number of ghost cells, and the MPI-AMRVAC 2.0 settings to run an actual application can now be specified in multiple parameter files.

A very important addition concerns regression tests for MPI-AMRVAC, in which their output is compared to stored "correct" results. We intend to have a least one such test for each type of major functionality that the code supports, varying dimensionality, equations to solve, or choice of algorithmic approach. The primary goal of these tests is to ensure that code changes do not affect the result of existing simulations. They can also help new users to explore MPI-AMRVAC's functionality, and to detect bugs and incompatibilities.

The implementation of these tests is as follows. First, a standard simulation is scaled down so that it can be run in a short time, e.g., one to ten seconds on a standard machine. We then specify the program to produce a log file of type "regression_test," which contains $\int {w}_{i}{dV}$ and $\int | {w}_{i}{| }^{2}{dV}$ over time, where ${\boldsymbol{w}}$ is a vector of the n_w (typically conservative) physical variables w_i per cell, for all variables $i\in [1,{n}_{w}]$. By comparing both the volume-integrated values of both cell values and their squares, errors in conservation properties and almost all errors in the shape of the solution are detected. The resulting log file is then compared to a previously stored version, using a finite error threshold in comparing values a to b as in:

$$\begin{eqnarray*}&&| a-b| \leqslant {\epsilon }_{\mathrm{abs}}+{\epsilon }_{\mathrm{rel}}(| a| +| b| )/2,\end{eqnarray*}$$

where we by default use an absolute tolerance of ${\epsilon }_{\mathrm{abs}}={10}^{-5}$ and relative tolerance of ${\epsilon }_{\mathrm{rel}}={10}^{-8}$. These tolerances account for changes due to numerical roundoff errors. Roundoff errors can for example occur when computations are re-ordered (using different compilation flags and/or compilers) or when a different number of processors is used. Most of the tests we have are performed for several combinations of numerical schemes. They can be executed automatically by running "make" in the tests folder of MPI-AMRVAC.

Having good documentation can increase the efficiency of both users and maintainers. However, as it takes considerable effort to write such documentation, this remains an ongoing process. For new contributions, we follow these guidelines for inline documentation:

• 1.  
  provide a short description of a non-trivial function/subroutine,
• 2.  
  when a piece of code is hard to understand, briefly describe what it does,
• 3.  
  variable names should be self-explanatory without getting lengthy.

For MPI-AMRVAC 2.0 we make use of Doxygen (see http://www.doxygen.org), so that most documentation can be written close to the code it documents. This helps when reading the code, but also makes it simpler to update documentation when changing code. The documentation is automatically generated every day and published on http://amrvac.org, which provides a starting point for new users.

MPI-AMRVAC can write output in several visualization formats, such as VTK or Tecplot. Furthermore, there is support for binary output files. These files can be used to restart a simulation, or to convert simulation data to any of the supported visualization file formats. For MPI-AMRVAC 2.0, we revised this binary format to make it future proof and simpler to use. The new binary format has a relatively simple structure, see Table 2, and it can be read and written with a modest amount of Fortran (or Python, C, etc.) code. Some of the changes with regards to the old format are:

• 1.  
  the introduction of a version number to provide backwards functionality,
• 2.  
  the header is now at the start of the file, to simplify reading files,
• 3.  
  byte offsets pointing to the location of the tree information and the block data allow new variables to be added at the end of the header,
• 4.  
  for each block, we also store its refinement, spatial index in the grid, and the location of its data, to facilitate reading in data,
• 5.  
  each grid block can now also store ghost cells.

We remark that the use of a format such as HDF5 would offer advantages in terms of standardization and portability. However, this would add a dependency on HDF5, which could complicate code installation and compilation for users and would require all our current tools for binary files to be rewritten.